Naif Bayes Sınıflandırması
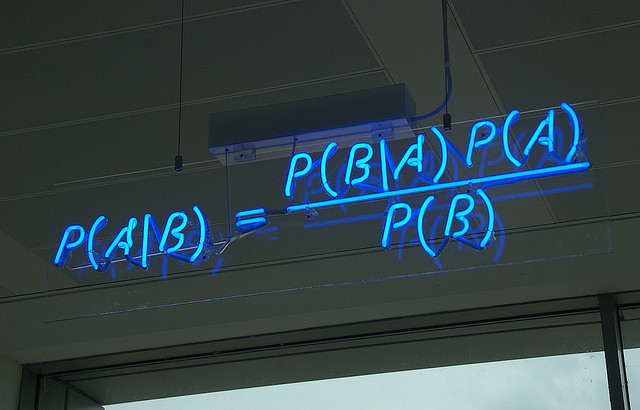
Naif bayes algoritması, istatistiksel bir sınıflandırma yöntemidir. Popüler bir olasılık teoremi olan bayes teoremine dayanır. Koşullu olasılık kavramı denmesi daha doğru olur.
Koşullu olasılık kavramını kısaca şöyle açıklayabiliriz. A ve B olayları olsun. B olayı gerçekleştiğinde A olayının gerçekleşme olasılığının hesaplanmasıdır. Gözetimli bir öğrenme şekli olan naif bayes algoritması işte bunun çözümü sağlıyor. Peki bu nasıl oluyor? Aşağıdaki formül ile;
P(A|B) = P(B|A) * P(A) / P(B)
P(A|B) : B olayı gerçekleştiğinde A olayının gerçekleşme olasılığı
P(B|A) : A olayı gerçekleştiğinde B olayının gerçekleşme olasılığı
P(A) : A olayının gerçekleşme olasılığı
P(B) : B olayının gerçekleşme olasılığı
Bağımlı değişken ile bağımsız değişkenler arasındaki koşullu olasılık hesabı yapılıp daha sonra bu tersine çevrilip hesaplanması yapılıyor ve sonuca en fazla etki eden değişkenler tespit ediliyor. Bağımlı değişken formüldeki A , yani sonuçtur. Daha sonra bağımsız değişkenler olarak ele aldığımız durumları hesaplarız. Bu değişkenler arasındaki olasılık hesabı yapılıp koşullu olasılığı hesaplanır. Naif kelimesi bağımsız değişkenlerin tek başına hesaplanmasından gelir.
Naif bayes algoritması anladığım kadarı ile en çok kullanıldığı alanlardan birisi tıp alanındadır. Örnek bazı semptomlar sonucu hastalıkların tanımlaması gibi. Bir başka örnek ise gelen maillerin içeriğine göre spam olup olmayacağı sınıflandırılması diyebiliriz.
Bir örnek verelim. Udemy’de bir kursu satıyor olalım ve elimizde 3 tane parametremiz olsun. Bunlar yaş, cinsiyet, öğrenci olup olmadığı. Aşağıdaki bir gibi veri setimiz olsun.
| öğrenci mi? | yaş aralığı | cinsiyet | satıldı mı? |
|---|---|---|---|
| evet | [18, 25] | erkek | hayır |
| evet | [25, 35] | erkek | evet |
| evet | [25, 35] | kadın | hayır |
| hayır | [18, 25] | erkek | hayır |
| hayır | [35, 45] | erkek | evet |
| hayır | >45 | erkek | hayır |
| evet | [18, 25] | kadın | evet |
| hayır | >45 | kadın | hayır |
| evet | [18, 25] | erkek | evet |
| evet | [18, 25] | erkek | evet |
Bu grafiğe göre alıp ve almama oranını bulalım.
P(kursu satın alanlar) = 6/10 = 0.6
P(kursu satın almayanlar) = 4/10 = 0.4
Bir kişinin dersi incelediğini varsayalım. Özellikleri şöyle olsun. 24 yaşında erkek bir öğrenci. Tek tek alacağı ve almayacağı olasılıklarını hesaplayalım.
P(her değişkenin durumu \| kursu alıp almama)
P(öğrenci: evet | satın aldı) = 4/10 = 0.4
P(öğrenci: hayır | satın almadı) = 6/10 = 0.6
P(yaş aralığı: [18,25] | satın aldı) = 3/10 = 0.3
P(yaş aralığı: [18,25] aralığında değil | satın almadı) = 7/10 = 0.7
P(cinsiyet: erkek | satın aldı) = 4/10 = 0.6
P(cinsiyet: erkek | satın almadı) = 6/10 = 0.4
Daha sonra;
Bütün değişkenler ile alma olasılığı: 0.4 * 0.3 * 0.6 = 0.072
Bütün değişkenler ile almama olasılığı: 0.4 * 0.7 * 0.4 = 0.112
Daha sonra toplam kursu satın alma ve almama olasılıkları ile çarpıyoruz.
Satın alma ihtimalinin sonucu = 0.072 * 0.6 = 0.0432
Satın almama ihtimalinin sonucu = 0.112 * 0.4 = 0.0448
Buradaki değerler tamamen rastgele olduğu için sonuçta birbirine çok yakın denk geldi. Burada 24 yaşında erkek bir öğrencinin bizim kursumuzu alma ihtimali alma ihtimalinden düşük çıkıyor. Eğer tam tersi olsaydı ona bir indirim gösterip almasını sağlayabilirdik.
kaynaklar
- How To Implement Naive Bayes From Scratch in Python
- Her sakallıyı baban sanma: Temel oranı ihmal yanılgısı
- Naif Bayes Sınıflandırıcısı (Naive Bayes)